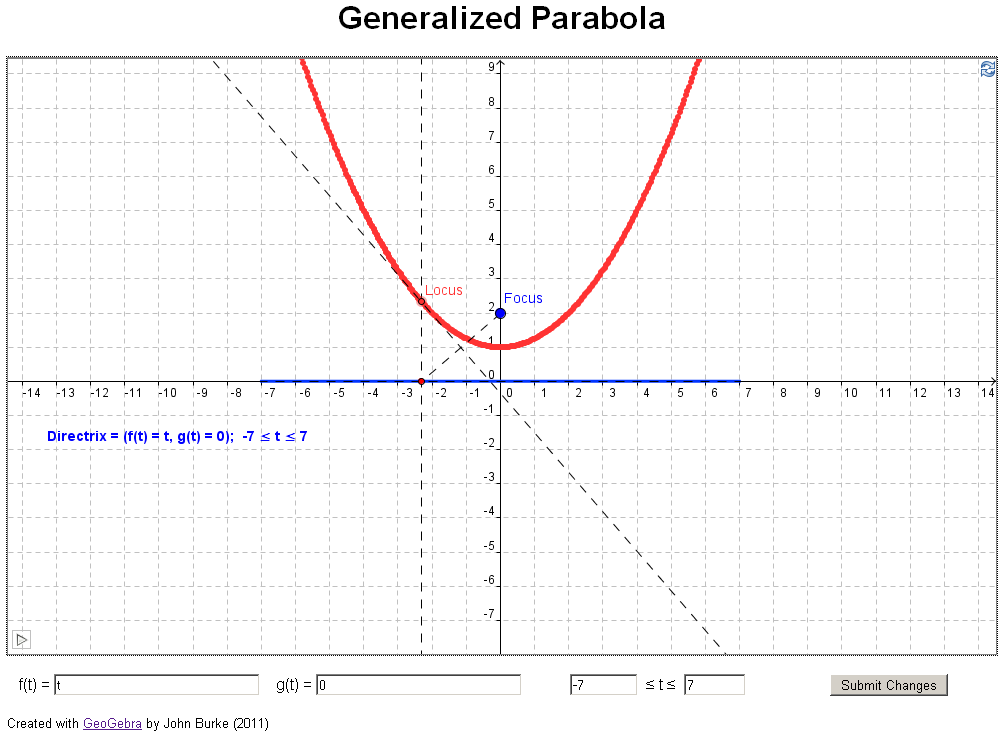
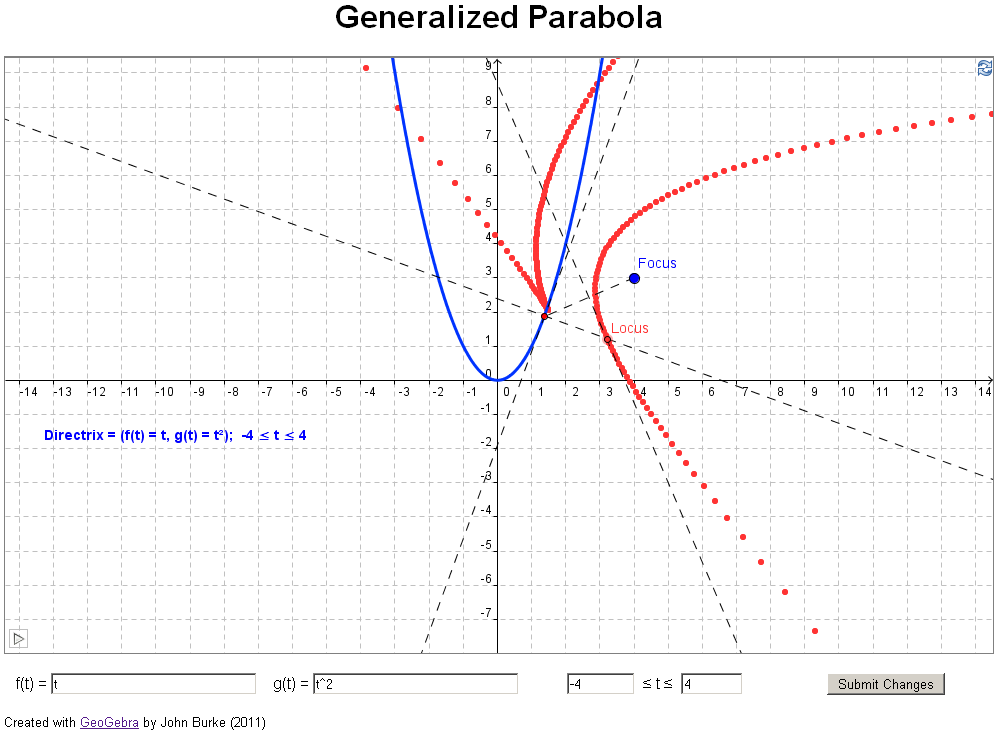
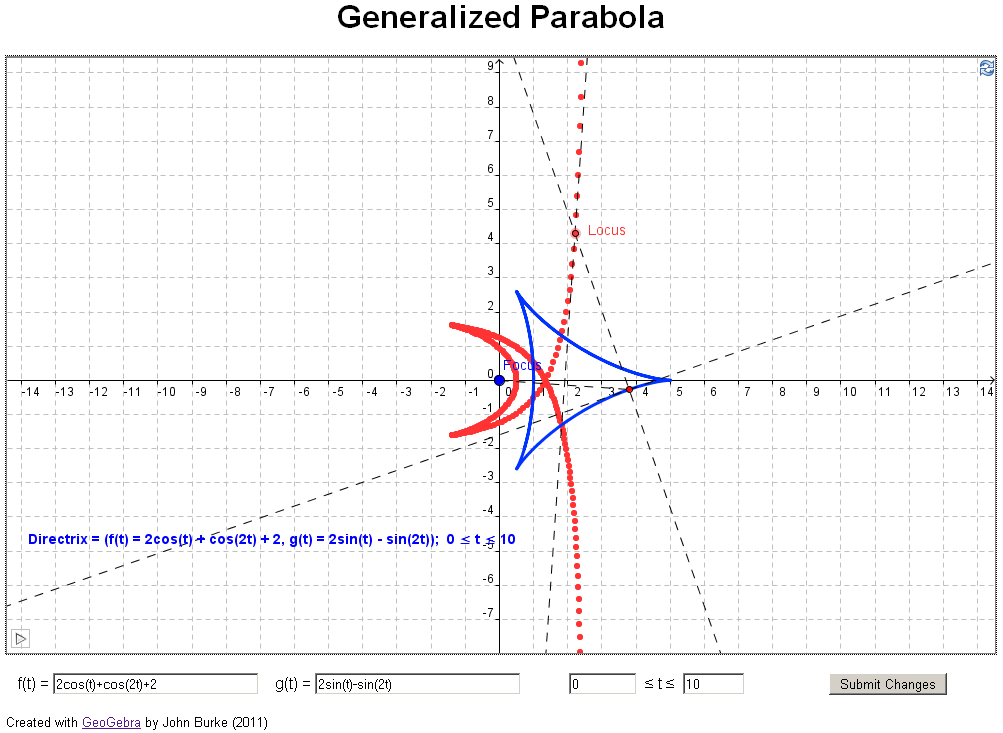
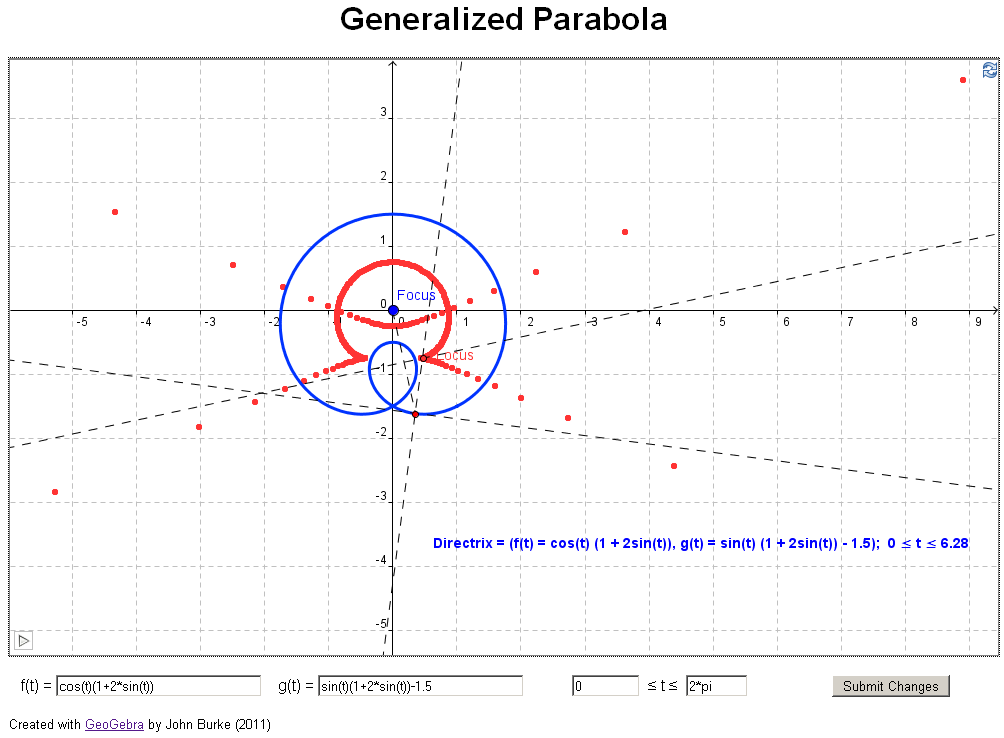
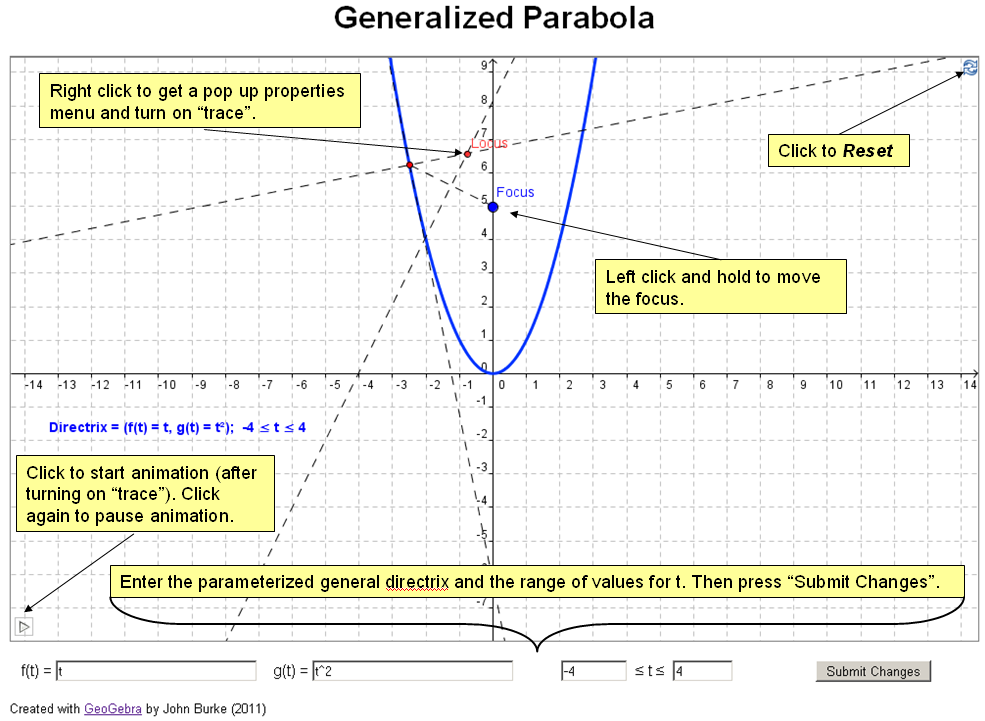
A
parabola is the locus of all points equidistant from a
given point, the focus, and a line, the
directrix.
The
September 2011 issue of The College Mathematics Journal
(published by MAA) contains an article by Dan Joseph,
Gregory Hartman and Caleb Gibson titled Generalized
Parabolas (available online if a member/subscriber or
through jstor:
http://www.jstor.org/pss/10.4169/college.math.j.42.4.275
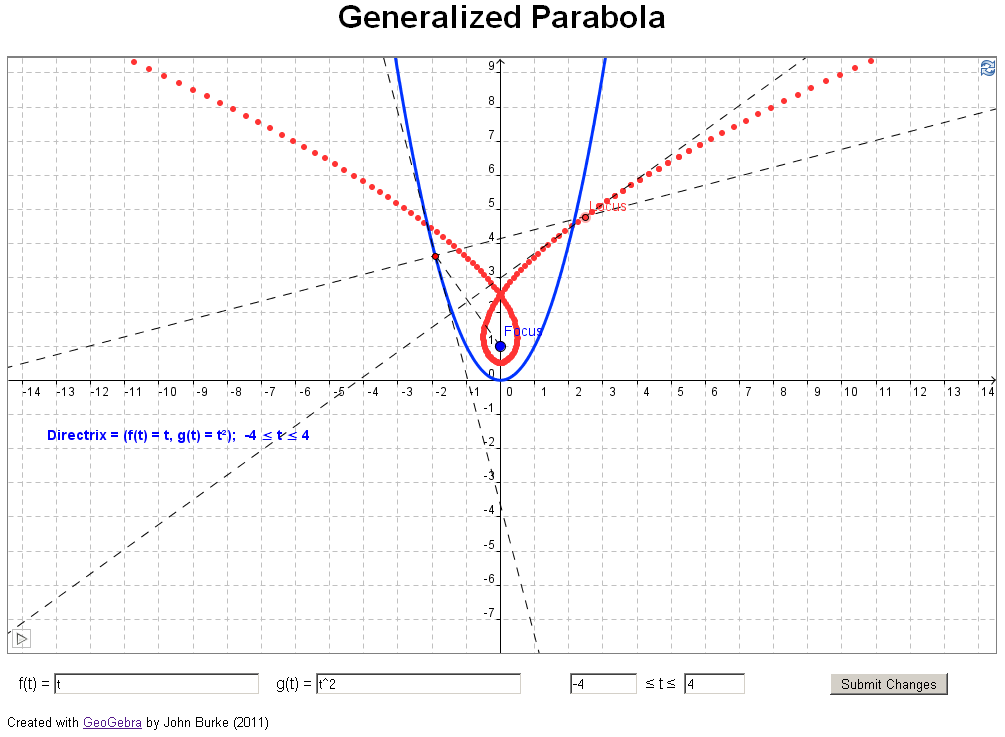
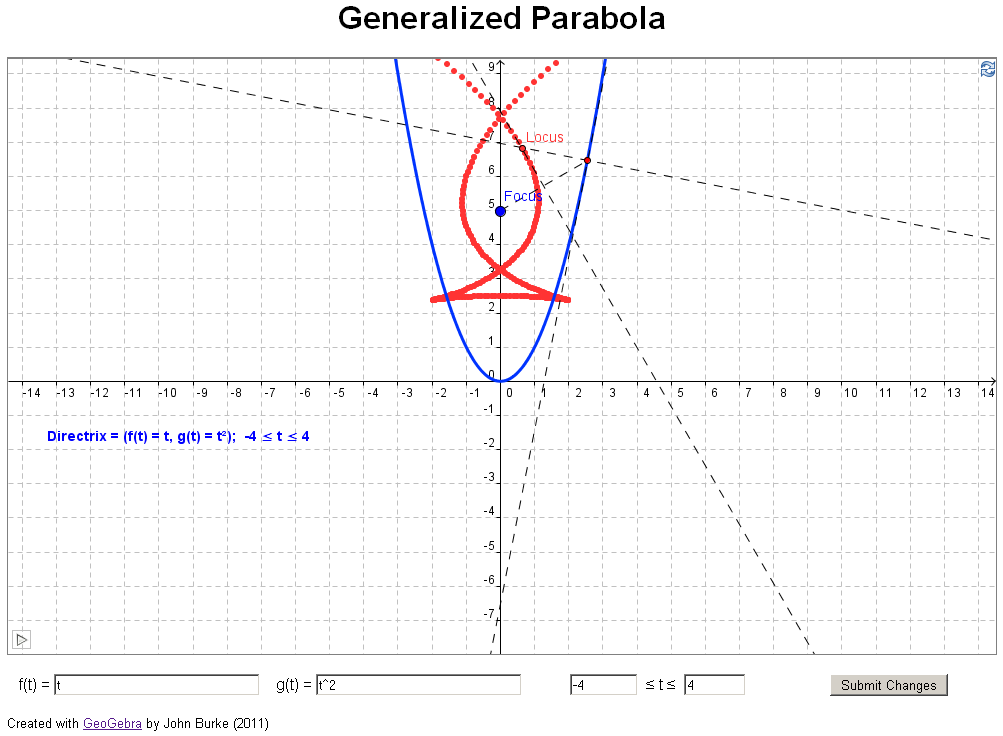
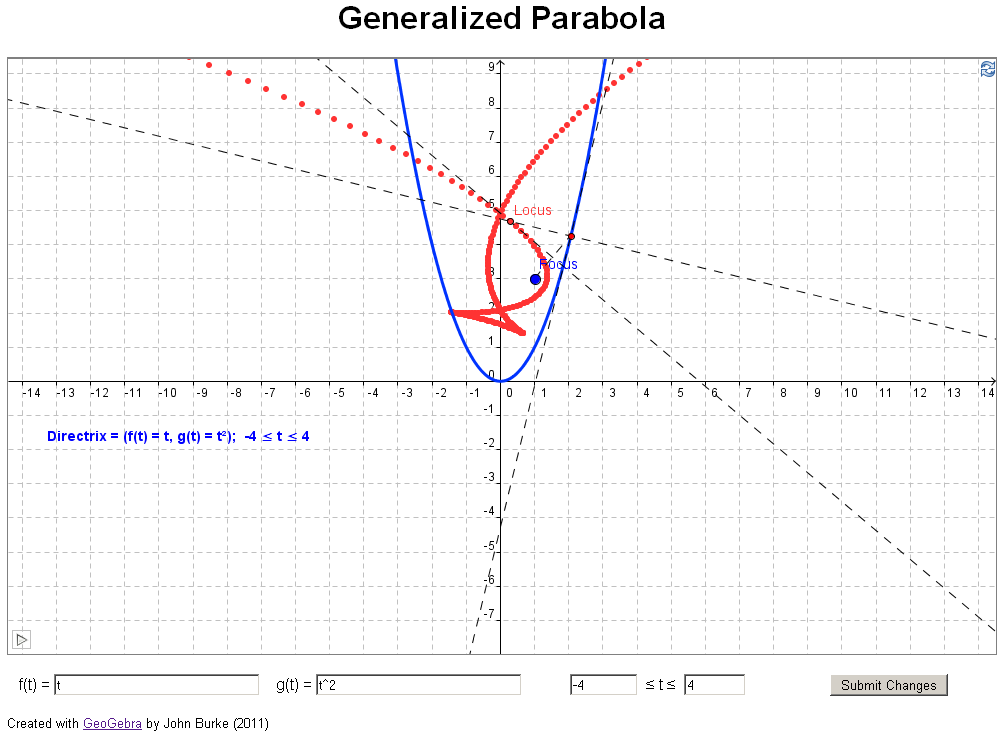
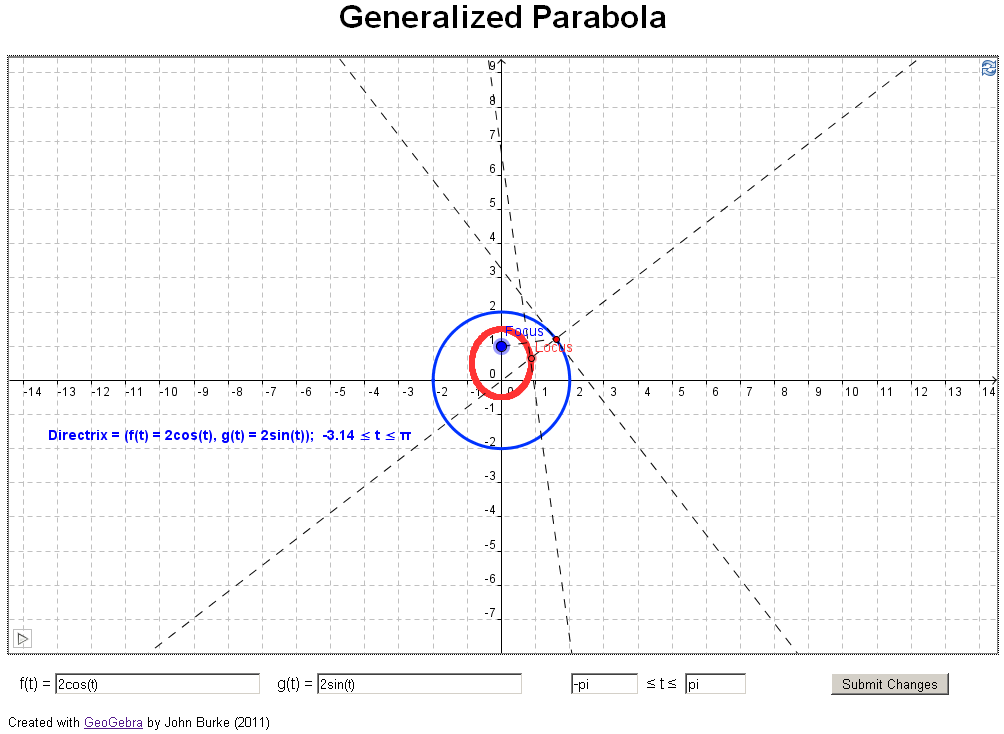
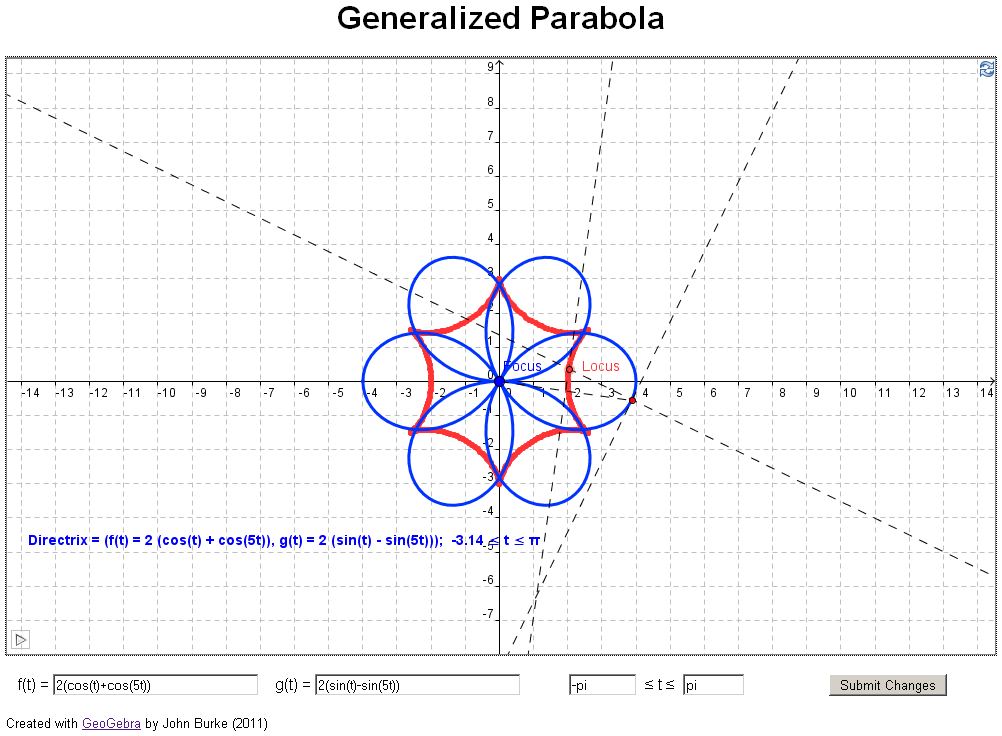
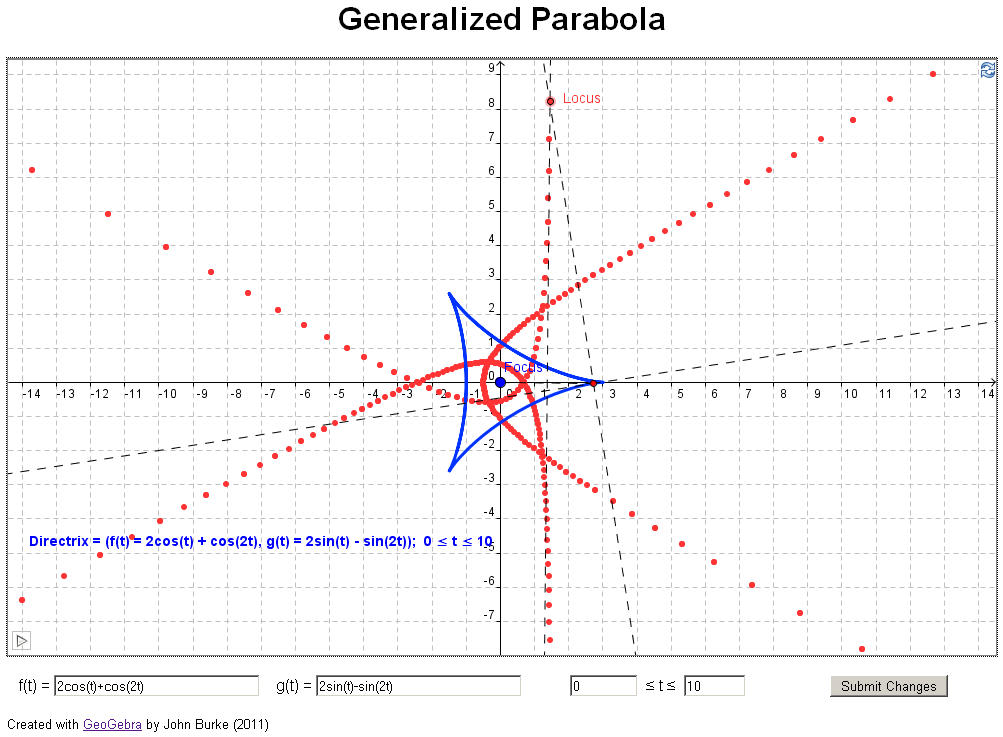
if you have access to jstor). In their article they investigate what happens if you
change the directrix in the definition above to a
general curve, for example, a parabola (see example 3
below). The authors took an analytical approach, using
Mathematica to find the equation of each generalized
parabola.
I
recognized GeoGebra could be used for a purely
geometrical investigation. Examples 3 through 11 below
reproduce examples from the paper sited above.
The
routine that produced the examples below is available
for use
here.
Example 1 gives some
instructions on using the generalized parabolas GeoGebra
manupulative. |